A simulation introduction to censoring in survival analysis

In teaching some students about survival analysis methods this week, I wanted to demonstrate why we need to use statistical methods that properly allow for right censoring. This post is a brief introduction, via a simulation in R, to why such methods are needed.

To do this, we will simulate a dataset first in which there is no censoring. We first define a variable n for the sample size, and then a vector of true event times from an exponential distribution with rate 0.1:

n <- 10000
set.seed(123)
eventTime <- rexp(n,0.1)

At the moment, we observe the event time for all 10,000 individuals in our study, and so we have fully observed data (no censoring). Because the exponentially distributed times are skewed (you can check with a histogram), one way we might measure the centre of the distribution is by calculating their median, using R’s quantile function:

quantile(eventTime, 0.5)

     50% 
6.985061 

Since we are simulating the data from an exponential distribution, we can calculate the true median event time, using the fact that the exponential’s survival function is . If we set and solve the equation for , we obtain for the median survival time. With our value of this gives us

-log(0.5)/0.1

6.931472

Our sample median is quite close to the true (population) median, since our sample size is large.

Adding in censoring

Now let’s introduce some censoring. Let’s suppose our study recruited these 10,000 individuals uniformly during the year 2017. To simulate this, we generate a new variable recruitDate as follows:

recruitDate <- 2017+runif(n)

We can then plot a histogram to check the distribution of the simulated recruitment calendar times:

hist(recruitDate)

Next we add the individuals’ recruitment date to their eventTime to generate the date that their event takes place:

eventDate <- recruitDate + eventTime

Now let’s suppose that we decide to stop the study at the end of 2019/start of 2020. In this case for those individuals whose eventDate is less than 2020, we get to observe their event time. But for those with an eventDate greater than 2020, their time is censored. We therefore generate an event indicator variable dead which is 1 if eventDate is less than 2020:

dead <- 1*(eventDate<2020)

We can now construct the observed time variable. For those with dead==1, this is their eventTime. For those with dead==0, this is the time at which they were censored, which is the difference between their recruitDate and 2020. We thus generate a new variable t as:

t <- eventTime
t[dead==0] <- 2020-recruitDate[dead==0]

Now let’s take a look at the variables we’ve created, with:

> head(cbind(recruitDate,eventTime,dead,t))

     recruitDate  eventTime dead          t
[1,]    2017.961  8.4345726     0 2.0390342
[2,]    2017.277  5.7661027     0 2.7230049
[3,]    2017.702 13.2905487     0 2.2977629
[4,]    2017.959  0.3157736     1 0.3157736

[5,]    2017.705  0.5621098     1 0.5621098
[6,]    2017.797  3.1650122     0 2.2026474

The data we would observe in practice would be each person’s recruitDate, their value of the event indicator dead, and the observed time t. As the above shows, for those individuals with dead==1, the value of t is their eventTime. For those with dead==0, t is equal to the time between their recruitment and the date the study stopped, at the start of 2020.

Next, let’s consider some simple but naive ways of handling the right censoring in the data when trying to estimate the median survival time.

Ignoring the event indicator

One simple approach would be to ignore the censoring completely, in the sense of ignoring the event indicator variable dead. Thus we might calculate the median of the observed time t, completely disregarding whether or not t is an event time or a censoring time:

quantile(t, 0.5)
     
50% 
2.365727 

Our estimated median is far lower than the estimated median based on eventTime before we introduced censoring, and below the true value we derived based on the exponential distribution. This happens because we are treating the censored times as if they are event times. For those individuals censored, the censoring times are all lower than their actual event times, some by quite some margin, and so we get a median which is far too small.

Ignoring the censored observations

An arguably somewhat less naive approach would be to calculate the median based only on those individuals who are not censored. If we view censoring as a type of missing data, this corresponds to a complete case analysis or listwise deletion, because we are calculating our estimate using only those individuals with complete data:

quantile(t[dead==1], 0.5)
     
50% 

1.178013 

Now we obtain an estimate for the median that is even smaller – again we have substantial downward bias relative to the true value and the value estimated before censoring was introduced. The reason for this large downward bias is that the reason individuals are being excluded from this analysis is precisely because their event times are large. We are estimating the median based on a sub-sample defined by the fact that they had the event quickly. As such, we shouldn’t be surprised that we get a substantially biased (downwards) estimate for the median.

Properly accounting for censoring

To properly allow for right censoring we should use the observed data from all individuals, using statistical methods that correctly incorporate the partial information that right-censored observations provide – namely that for these individuals all we know is that their event time is some value greater than their observed time. We can do this in R using the survival library and survfit function, which calculates the Kaplan-Meier estimator of the survival function, accounting for right censoring:

library(survival)
km <- survfit(Surv(t,dead)~1)
km

Call: survfit(formula = Surv(t, delta) ~ 1)

      n  events  median 0.95LCL 0.95UCL
 
  10000    2199      NA      NA      NA 

This output shows that 2199 events were observed from the 10,000 individuals, but for the median we are presented with an NA, R’s missing value indicator. Why? Plotting the Kaplan-Meier curve reveals the answer:

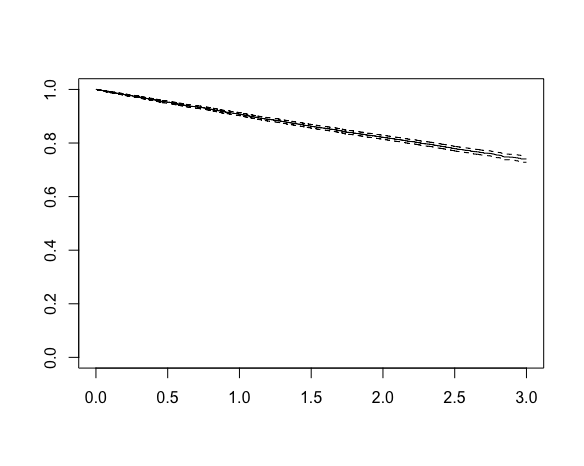
The x-axis is time and the y-axis is the estimate survival probability, which starts at 1 and decreases with time. We see that the x-axis extends to a maximum value of 3. This is because we began recruitment at the start of 2017 and stopped the study (and data collection) at the end of 2019, such that the maximum possible follow-up is 3 years. The curve declines to about 0.74 by three years, but does not reach the 0.5 level corresponding to median survival. This explains the NA for the median – we cannot estimate the median survival time based on these data, at least not without making additional assumptions. The Kapan-Meier estimator is non-parametric – it does not assume a particular distribution for the event times.

If we were to assume the event times are exponentially distributed, which here we know they are because we simulated the data, we could calculate the maximum likelihood estimate of the parameter , and from this estimate the median survival time based on the formula derived earlier. The Kaplan-Meier curve visually makes clear however that this would correspond to extrapolation beyond the range of the data, which we should only data in practice if we are confident in the distributional assumption being correct (at least approximately).