Disclaimer: I am in absolutely no way an expert on Covid-19 or tests for it. This post was motivated from undergraduate teaching for medical statistics, and probably makes assumptions which are implausible.
This morning I spoke to my undergraduate medical statistics students briefly about this piece in the BMJ published a few days ago raising concerns about the possible low test sensitivity of the rapid lateral flow tests which are being used in various contexts currently in the UK. This piece cites a UK government document which says concerning the lateral flow tests that:
Results of the PHE and Oxford University Innova evaluation show it has an overall analytical sensitivity of 76.8% for all PCR-positive individuals but detects over 90% of individuals with high viral loads
https://www.gov.uk/government/publications/community-testing-explainer/community-testing-a-guide-for-local-delivery#what-the-community-testing-programme-is
and that
In field evaluations, such as Liverpool, these tests still perform effectively and detect at least 50% of all PCR positive individuals and more than 70% of individuals with higher viral loads in both symptomatic and asymptomatic individuals.
https://www.gov.uk/government/publications/community-testing-explainer/community-testing-a-guide-for-local-delivery#what-the-community-testing-programme-is
The concern then is that these lateral flow tests have quite low sensitivity, and hence that they may wrongly give negative test results to a substantial fraction of those who are truly infected.
But this got me thinking – the sensitivity figures being quoted here are taking (as far as I can see, but I may be wrong here) the PCR test result as the true infection status, when of course this test itself has imperfect sensitivity and specificity. Given this, part of the poor sensitivity estimates for the lateral flow test could be attributable to the imperfect sensitivity and specificity of the PCR tests. A natural question then is, what might the true sensitivity of the lateral flow tests be, defined as the fraction of truly infected individuals who would get a positive lateral flow test?
One way of getting at this is to calculate what the apparent sensitivity of the lateral flow test would be under various assumptions for the two tests’ sensitivities, specificities and population prevalence of infection. We can do this under an assumption (which could very well be false for all I know) that the PCR and lateral flow test results are conditionally independent given someone’s true infection status.
Let D denote the true infection status of an individual (1 for truly infected, 0 for not), T1 the PCR test result (1 for positive, 0 for negative), and T2 for the lateral flow test result. A bit of conditional probability then shows that the apparent sensitivity of the lateral flow test, taking the PCR test as if it were true infection status, is:
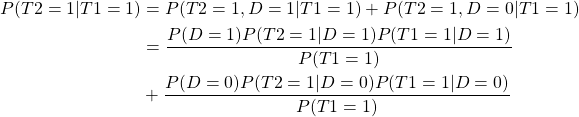
which we can write as
![]()
where p denotes the population prevalence of infection, Se1 and Sp1 denote the sensitivity and specificity of the PCR test, and Se2 and Sp2 denote the sensitivity and specificity of the lateral flow test.
The Google Sheet accessible here implements this formula, so we can see what the impact of using the PCR test test as the gold standard might be on the apparent sensitivity of the lateral flow test under various assumptions. Suppose the population prevalence of infection is 1%, the PCR sensitivity is 95% and its specificity is 99.9%, and the lateral flow test has sensitivity and specificity (defined using the true infection status) of 95%. Then the apparent sensitivity of the lateral flow test reduces to 86.5%. But if we reduce the specificity of the PCR test down just a little bit 99.0%, so we get more PCR false positives, the apparent sensitivity of the lateral test reduces to just 49%, even if in truth its sensitivity for detecting true infection were 95%. This is quite a dramatic reduction, and I wondered after my teaching this morning if this at least partly explains the apparent low sensitivity of the lateral flow tests.
As per the disclaimer at the top, I am not an expert in any way on Covid-19 testing or diagnostics, and I have no doubt the above considerations are already very well understood by those concerned with developing and evaluating the tests. If as is likely I have made some poor or stupid assumptions, please let me know in a comment.
Postscript (11th December 2020)
As I was hoping, people who know more about these things than me helpfully explained on Twitter that in countries like Australia and New Zealand we’ve seen very low total positive rates, and the false positive rate (1-specificity) can be no larger than the total positive rate. Using OurWorldInData, for New Zealand we can see the positive test rate over the last few months below, which shows it has never been above 0.1% over this period. If the false positive rate were 0.1%, this would indeed suggest that the idea put forward in this post would not be a major contributor to the apparent sensitivity of lateral flow test being low, when evaluated using the PCR result as if it were true infection status.