Regression inference assuming predictors are fixed

by

Linear regression is one the work horses of statistical analysis, permitting us to model how the expectation of an outcome Y depends on one or more predictors (or covariates, regressors, independent variables) X. Previously I wrote about the assumptions required for validity of ordinary linear regression estimates and their inferential procedures (tests, confidence intervals) assuming (as we often do) that the residuals are normally distributed with constant variance.

In my experience, when the ordinarily least squares (OLS) estimators and inferential procedures for them are taught to students, the predictors X are treated as fixed. That is, we act as if they are controlled by the design of our study or experiment. In practice, in lots of studies the predictors are not under the control of the investigator, but are random variables like the outcome Y. As an example, suppose we are interested in finding out how blood pressure (BP) depends on weight. We take a random sample of 1000 individuals, and measure their BP and weight. We then fit a linear regression model with Y=BP and X=weight. The predictor X here is certainly not under the control of the investigator, and so it seems to me a quite reasonable question to ask: why is it valid to use inferential procedures which treat X as fixed, when in my study X is random?

First, lets consider the unbiasedness of the OLS estimators. Recall that the OLS estimators can be written as

\hat{\beta} = (\mathbf X^{T} \mathbf X)^{-1} \mathbf X^{T} \mathbf Y

where the bold Y and X denote the vector and matrix of the outcome and predictors respectively from our sample of subjects. Then under the assumption that E(Y|X)=X \beta, the OLS estimator \hat{\beta} is easily shown to be conditionally (on \mathbf X) unbiased, since:

E(\hat{\beta}|\mathbf X) = E((\mathbf X^{T} \mathbf X)^{-1} \mathbf X^{T} \mathbf Y | \mathbf X)=E((\mathbf X^{T} \mathbf X)^{-1} \mathbf X^{T} \mathbf X \beta | \mathbf X)=\beta

But what if our predictors are random? Then we are interested in the unconditional expectation of the estimator. In this case we can simply appeal to the rule of total expectation to see that

E(\hat{\beta})=E(E(\hat{\beta}|\mathbf X))=E(\beta)=\beta

What about the sampling variability of the OLS estimator? Assuming the residuals have constant variance \sigma^{2}, we can find its variance conditional on the observed values of the predictors by

Var(\hat{\beta}|\mathbf X)=Var((\mathbf X^{T} \mathbf X)^{-1} \mathbf X^{T} \mathbf Y|X)=(\mathbf X^{T} \mathbf X)^{-1} \mathbf X^{T} \sigma^{2} \mathbf X ((\mathbf X^{T} \mathbf X)^{-1})^{T}

which equals =\sigma^{2}(\mathbf X^{T} \mathbf X)^{-1}. In software, the variances of the OLS estimates are given using this formula, using the observed matrix \mathbf X and the sample estimate of the residual variance, s^{2}. But what about the unconditional variance of the estimator. Using the law of total variance we can find that

Var(\hat{\beta})=Var(E(\hat{\beta}|\mathbf X)) + E(Var(\hat{\beta}|\mathbf X))=Var(\beta)+ E(Var(\hat{\beta}|\mathbf X))=E(Var(\hat{\beta}|\mathbf X))=E(\sigma^{2}(\mathbf X^{T} \mathbf X)^{-1})

The unconditional variance of the OLS estimator is therefore the average, across samples in which X and Y are random, of the variance the OLS estimator would have for fixed X. It follows that using the usual OLS variance estimator, derived assuming fixed X, is an unbiased estimate of the unconditional variance of the estimator.

6 thoughts on “Regression inference assuming predictors are fixed”

  1. I think your discussion focused much on the properties of estimator but not really the fundamental differences between fixed and random regressors. Here are some of my thoughts concerning this issue:

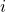    If we have stochastic regressors, we are drawing random pairs (y_i,\vec{x}_i) for a bunch of i, the so-called random sample, from a fixed but unknown probabilistic distribution 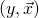(y,\vec{x}). Theoretically speaking, the random sample allows us to learn about or estimate some parameters of the distribution (y,\vec{x}).

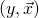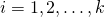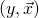    If we have fixed regressors, theoretically speaking, we can only infer certain parameters about k conditional distributions, y\mid x_i for i=1,2,\dots,k where each x_i is not a random variable, or is fixed. More specifically, stochastic regressors allow us to estimate some parameters of the entire distribution of (y,\vec{x}) while fixed regressors only let us estimate certain parameters of the conditional distributions (y,\vec{x_i})\mid x_i.

    The consequence is that fixed regressors cannot be generalized to the whole distribution. For example, if we only had x=1,2,3,\dots,99 in the sample as fixed regressors, we can not infer anything about 100 or 99.9, but stochastic regressors can.

    Nevertheless, I am still unsure of the validity of my argument. Would you mind providing more insights on this topic?

    Reply

  2. Thanks Kun for your very thought provoking comment! If we make no assumptions about how f(Y|X) depends on X, then I agree we can only estimate the conditional distribution of Y at those values of X which are used in the sample. However, lets suppose we are interested in modelling E(Y|X), i.e. how the mean of Y varies with X. Next suppose we are willing to make the assumption that E(Y|X) is linear in X. In this case we can identify the unknown parameters in this conditional mean model so long as we have observations of Y at at least two distinct values of X. The linearity assumption thus enables us to draw inferences about E(Y|X) for all values of X, but obviously the validity of this relies on the linearity assumption.

    Reply

  3. Thanks for your great discussion on treating $X$ as fixed or random regressors. I have one relevant question:

    In linear regression analysis, we sometimes do some transformation on covariates $X$. For example, centering $X$ at their means. The estimator of parameter of interest ($\hat{\theta}$) may contain these means. Once we replace them with sample means, should we adjust for the extra variability of estimated sample means in the variance estimator for ($\hat{\theta}$)? If we treat $X$ as fixed, I think their sample means should also be considered as fixed. So why we need to adjust for this extra variability when making conditional inference based on regression? Conditional inference is based on this conditional variance (($\hat{\theta|X}$)? There are other similar scenarios. For example, using some estimated variables as predictors (i.e, propensity scores).

    It would be great if you can share your thoughts on this.

    Reply

    • As you say, if the parameter of interest depends not only on parameters indexing the conditional distribution $Y|X$ but also on parameters (e.g. the mean) of the marginal distribution of the regressors, then in general I don’t think inference can be validly carried out treating the regressors as fixed (unless of course they are, or would be fixed in repeated sampling).

      As you allude, in cases such as propensity scores, where in the first stage the propensity scores are estimated, if one then uses the propensity scores in a second stage procedure, treating the estimated propensity scores as if they were just another variable you had collected does not in general lead to valid inferences. Paradoxically, in this case ignoring the first stage estimation leads to conservative inferences. A very good reference for this is Section 6 of Newey & McFadden’s 1994 book chapter in the Handbook of Econometrics IV, which can be viewed here.

      Reply

Leave a Reply

This site uses Akismet to reduce spam. Learn how your comment data is processed.