Robustness to misspecification when adjusting for baseline in RCTs

It is well known that adjusting for one or more baseline covariates can increase statistical power in randomized controlled trials. One reason that adjusted analyses are not used more widely may be because researchers may be concerned that results may be biased if the baseline covariate(s)’ effects are not modelled correctly in the regression model for outcome. For example, a continuous baseline covariate would by default be entered linearly in a regression model, but in truth it’s effect on outcome may be non-linear. In this post we’ll review an important result which shows that for continuous outcomes modelled with linear regression, this does not matter in terms of bias – we obtain unbiased estimates of treatment effect even if we mis-specify a baseline covariate’s effect on outcome.

Setup

We’ll assume that we have data from a two arm trial on $n$ subjects. For the ith subject we record a baseline covariate $X_{i}$ and outcome $Y_{i}$ . We let $Z_{i}$ denote a binary indicator of whether the subject is randomized to the new treatment group $Z_{i}=1$ or the standard treatment group $Z_{i}=0$ . In some situations the baseline covariate may be a measurement of the same variable (e.g. blood pressure) which is being measured at follow-up by $Y_{i}$ .

A linear regression model for the data is then specified as

$Y_{i} = \beta_{0} + \beta_{X} X_{i} + \beta_{Z} Z_{i} + \epsilon_{i}$

where $\epsilon_{i}$ are errors which have expectation zero conditional on $X_{i}$ and $Z_{i}$ . The parameters (regression coefficients) are then estimated using ordinary least squares. We let $\hat{\beta}_{Z}$ denote the estimated treatment effect. The true treatment effect is

$\Delta = E(Y_{i}|Z_{i}=1)-E(Y_{i}|Z_{i}=0) = \mu_{1}-\mu_{0}$

Robustness to misspecification

We now ask the question: is the ordinary least square estimator $\hat{\beta}_{Z}$ unbiased for $\Delta$ , even if the linear regression model assumed is not necessarily correctly specified? The answer is yes (asymptotically), and further below we outline the proof given by Yang and Tsiatis, in their 2001 paper ‘Efficiency Study of Estimators for a Treatment Effect in a Pretest-Posttest Trial’.

This means that for continuous outcomes analysed by linear regression, we do not need to worry that by potentially mis-specifying the $X_{i}$ effect we may introduce bias into the treatment effect estimator. The price of mis-specifying the effect of $X_{i}$ will be a reduction in efficiency. For more on methods which adaptively model this effect, see the 2008 paper by Tsiatis et al here and also Chapter 5 section 4 of Tsiatis’ book, ’Semiparametric Theory and Missing Data’. We also note a further results from Yang and Tsiatis, that in general a more efficient estimate can be obtained by allowing for an interaction between $X_{i}$ and treatment $Z_{i}$ .

Another important point to remember is that the standard ‘model based’ standard error from linear regression assumes that the residual errors have constant variance. If this assumption doesn’t hold, it’s important to account for this in our inferences. Providing the sample size is not small, this can be achieved by using sandwich standard errors, which I covered in an earlier post here.

Simulations

To illustrate these results, we perform a small simulation study. For trials of size $n=1,000$ , we will simulate the treatment indicator $Z_{i}$ and a baseline covariate $X_{i}$ . We will then simulate the outcome $Y_{i}$ from a linear regression model, but with linear and quadratic effects of $X_{i}$ . The true treatment effect is set to $\Delta=1$ .

We perform three analyses: 1) an unadjusted analysis using lm(), equivalent to a two sample t-test, 2) an adjusted analysis, including $X_{i}$ linearly, and hence mis-specifying the outcome model, and 3) the correct adjusted analysis, including both linear and quadratic effects of $X_{i}$ .

The code is given by:

nsim <- 1000

n <- 1000
pi <- 0.5

unadjusted <- array(0, dim=nsim)
adjustedmisspec <- array(0, dim=nsim)
adjustedcorrspec <- array(0, dim=nsim)

for (sim in 1:nsim) {

z <- rbinom(n, 1, pi)
x <- rnorm(n)

y <- x+x^2+z+rnorm(n)

#analysis not adjusting for baseline
unadjustedMod <- lm(y~z)
unadjusted[sim] <- coef(unadjustedMod)[2]

#adjusted analysis misspecified
adjustedmisspecMod <- lm(y~z+x)
adjustedmisspec[sim] <- coef(adjustedmisspecMod)[2]

#adjusted correctly specified
xsq <- x^2
adjustedcorrspecMod <- lm(y~z+x+xsq)
adjustedcorrspec[sim] <- coef(adjustedcorrspecMod)[2]

}

mean(unadjusted)
mean(adjustedmisspec)
mean(adjustedcorrspec)

sd(unadjusted)
sd(adjustedmisspec)
sd(adjustedcorrspec)

Running this, I obtained (without setting the seed, you will get slightly different results):


> mean(unadjusted)
[1] 0.9988225
> mean(adjustedmisspec)
[1] 0.9980142
> mean(adjustedcorrspec)
[1] 0.9995535
> sd(unadjusted)
[1] 0.121609
> sd(adjustedmisspec)
[1] 0.1090832
> sd(adjustedcorrspec)
[1] 0.0639239

As expected, all three estimators are unbiased. In particular, the estimator based on a mis-specified adjustment for the baseline covariate remains unbiased, as per the theory. Moreover, we see that even with the mis-specified model, the estimator is less variable than the unadjusted estimator, corresponding to a gain in efficiency. However, we also see that a much larger efficiency gain is possible if we are able to correctly specify the effect of the baseline covariate.

Proof

The following proof is taken from a 2001 paper by Yang and Tsiatis, which can be accessed at JSTOR here. First we centre all three variables. The variables centred by their true expectations are denoted $Y^{*}_{i}=Y_{i}-E(Y_{i})$ , $X^{*}_{i}=X_{i}-E(X_{i})$ and $Z^{*}_{i}=Z_{i}-E(Z_{i})$ . We let $Y^{C}_{i},X^{C}_{i},Z^{C}_{i}$ denote the variables centred by their sample (as opposed to population) means. After centreing, our model for the variables centred about their population means becomes

$Y^{*}_{i} = \beta_{X}X^{*}_{i} + \beta_{Z} Z^{*}_{i} + \epsilon_{i}$

where now there is no intercept because of the centreing. Note also that after centreing the variables about their corresponding sample means, we can fit the model to the empirically centred variables $Y^{C}_{i},X^{C}_{i},Z^{C}_{i}$ without an intercept, and obtain the same estimates $\hat{\beta}_{Z}$ and $\hat{\beta}_{Z}$ as without centreing. We now let $D^{*}_{i}=(X^{*}_{i},Z^{*}_{i})^{T}$ and $D^{C}_{i}=(X^{C}_{i},Z^{C}_{i})^{T}$ . The OLS estimators can then be expressed as

$\begin{pmatrix}\hat{\beta}_{X} \\ \hat{\beta}_{Z} \end{pmatrix} = \left\{ \sum^{n}_{i=1} D^{C}_{i} D^{C^{T}}_{i} \right\}^{-1} \left\{ \sum^{n}_{i=1} D^{C}_{i} Y^{C}_{i} \right\}$

As the sample size tends to infinity, the OLS estimators converge in probability to

$\begin{pmatrix}\hat{\beta}_{X} \\ \hat{\beta}_{Z} \end{pmatrix} \overset{p}{\rightarrow} \left\{ E\left( D^{*}_{i} D^{*^{T}}_{i} \right) \right\}^{-1} \left\{ E \left( D^{*}_{i} Y^{*}_{i} \right) \right\}$

We can then derive

$E\left( D^{*}_{i} D^{*^{T}}_{i} \right) = \begin{pmatrix} E(X^{*^{2}}_{i}) & E(X^{*}_{i}Z^{*}_{i}) \\ E(X^{*}_{i}Z^{*}_{i}) & E(Z^{*^{2}}) \end{pmatrix}$

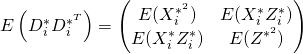
Then we have that since $X^{*}_{i}$ has mean zero, $E(X^{*^{2}}_{i}) = Var(X^{*}_{i}) = \sigma^{2}_{X}$ . Since $Z^{*}_{i}=Z_{i}-0.5$ and similarly has mean zero, $E(Z^{*^{2}}_{i}) = Var(Z^{*^{2}}_{i}) = \pi \times (1-\pi)$ where $\pi=P(Z_{i}=1)$ . Lastly, by randomization, $X^{*}_{i}$ and $Z^{*}_{i}$ are statistically independent, which means that $E(X^{*}_{i} Z^{*}_{i}) = 0$ . Since the off diagonal elements are zero, we then have that

$\hat{\beta}_{Z} \overset{p}{\rightarrow} \left\{ E(Z^{*^{2}}) \right\}^{-1} E(Z^{*}_{i} Y^{*}_{i}) = (\pi(1-\pi))^{-1} E(Z^{*}_{i} Y^{*}_{i})$

To find the latter expectation we can use the law of total expectation to give

$E(Z^{*}_{i} Y^{*}_{i}) = E(E(Z^{*}_{i}Y^{*}_{i}|Z_{i})) = E((Z_{i}-\pi)E(Y^{*}_{i}|Z_{i}))$

Since we can write $Y_{i}=\mu_{0} + \Delta Z_{i} + error$ and $E(Y_{i}) = \mu_{0} + \Delta \pi$ , we have that

$E(Y^{*}_{i}|Z_{i}) = \Delta(Z_{i}-\pi)$

and so

$E(Z^{*}_{i} Y^{*}_{i}) = E((Z_{i}-\pi)^{2} \Delta) = \Delta \pi (1-\pi)$

Finally then, we have

$\hat{\beta}_{Z} \overset{p}{\rightarrow} (\pi(1-\pi))^{-1} E(Z^{*}_{i} Y^{*}_{i}) = (\pi(1-\pi))^{-1} \pi (1-\pi) \Delta = \Delta$

We have thus shown that the OLS estimate of treatment effect is consistent for $\Delta$ irrespective of whether the linearity assumption for the baseline covariate's effect on $Y_{i}$ is correct or not.

Robustness to misspecification when adjusting for baseline in RCTs

Setup

Robustness to misspecification

Simulations

Proof

You may also be interested in:

Leave a ReplyCancel reply