Previously I wrote about how when linear regression is introduced and derived, it is almost always done assuming the covariates/regressors/independent variables are fixed quantities. As I wrote, in many studies such an assumption does not match reality, in that both the regressors and outcome in the regression are realised values of random variables. I showed that the usual ordinary least squares (OLS) estimators are unbiased with random covariates, and that the usual standard error estimator, derived assuming fixed covariates, is unbiased with random covariates. This gives us some understand of the behaviour of these estimators in the random covariate setting.
Here I’ll take a different approach, and appeal to the powerful theory of estimating equations. It turns out that many of the statistical estimators we use can be expressed as being the solutions to a set of estimating equations. The theory is powerful because it allows us to derive the asymptotic (large sample) behaviour of the estimators, and also gives us a consistent estimator of variance (of the parameter estimator), enabling us to find standard errors and confidence intervals. An excellent article introducing this theory, by Stefanski and Boos, can be found here. For further details, I’d highly recommend Tsiatis’ book ’Semiparametric Theory and Missing Data’, which covers estimating equation theory in semiparametric models.
To recall the linear regression, suppose we have, for each subject, an outcome Y and vector of predictors X. To keep the derivations simple, I will assume the first component of X includes 1, representing a constant intercept. The fundamental modelling assumption is then that ![]() , where
, where ![]() is a column vector of regression coefficients to be estimated. The OLS estimator of
is a column vector of regression coefficients to be estimated. The OLS estimator of ![]() is usually expressed as:
is usually expressed as:
![]()
where bold ![]() and
and ![]() respectively denote the vector and matrix containing the values of Y and X for all n subjects in the sample. It is easy to show that the OLS estimator is also given by the value of
respectively denote the vector and matrix containing the values of Y and X for all n subjects in the sample. It is easy to show that the OLS estimator is also given by the value of ![]() which solves the following estimating equation:
which solves the following estimating equation:
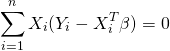
where ![]() and
and ![]() denote the values of Y and X for the ith subject.
denote the values of Y and X for the ith subject.
Asymptotic distribution
Now we can begin to start applying the theory of estimating equations. First, under certain regularity conditions, the theory tells that the distribution of the estimator ![]() converges to that of a (multivariate) normal distribution as the sample size n tends to infinity. Importantly, this holds irrespective of whether the errors
converges to that of a (multivariate) normal distribution as the sample size n tends to infinity. Importantly, this holds irrespective of whether the errors ![]() are normally distributed or not, and also irrespective of whether they have constant variance.
are normally distributed or not, and also irrespective of whether they have constant variance.
Consistency
Next, theory says that the estimator will be consistent if the estimating function, which here is ![]() , has expectation zero when evaluated at the true value of
, has expectation zero when evaluated at the true value of ![]() . Consistency means that for large sample sizes, the estimator will be close to the true population parameter value with high probability. To check that this condition holds for the OLS estimators, we must find the expectation
. Consistency means that for large sample sizes, the estimator will be close to the true population parameter value with high probability. To check that this condition holds for the OLS estimators, we must find the expectation ![]() . To do this, we make use of the law of total expectation:
. To do this, we make use of the law of total expectation:
![]()
If the model is correctly specified, ![]() , and so
, and so ![]() . The estimating function thus has mean zero. We can therefore conclude the OLS estimator is consistent for
. The estimating function thus has mean zero. We can therefore conclude the OLS estimator is consistent for ![]() .
.
Variance
We now turn to the variance of the estimator. Without for the moment making any further assumptions other than that ![]() , estimating equation theory says that with a sample size of n, the estimator has variance
, estimating equation theory says that with a sample size of n, the estimator has variance
![]()
where ![]() denotes the matrix is equal to minus the derivative of the estimating function with respect to the parameter
denotes the matrix is equal to minus the derivative of the estimating function with respect to the parameter ![]() ,
, ![]() denotes the variance covariance matrix of the estimating function, and
denotes the variance covariance matrix of the estimating function, and ![]() denotes the true value of
denotes the true value of ![]() . First we find the second of these matrices, using the law of total variance
. First we find the second of these matrices, using the law of total variance
![Rendered by QuickLaTeX.com \begin{eqnarray*} B(\beta)&=&Var(X(Y-X^{T}\beta))\\ &=& E\left[Var(X(Y-X^{T}\beta)|X)\right] +Var\left[E(X(Y-X^{T}\beta)|X)\right] \end{eqnarray*}](https://thestatsgeek.com/wp-content/ql-cache/quicklatex.com-26d6721dfbbeca0bfb787d8cf7a080b8_l3.png)
Since ![]() , the second term here is zero. If we write
, the second term here is zero. If we write ![]() , we have
, we have
![]()
In this post, let’s suppose the errors have constant variance (I’ll come back to the non-constant variance case in a later post), so that ![]() . Then
. Then
![]()
Turning now to the matrix ![]() , taking minus the derivative (with respect to
, taking minus the derivative (with respect to ![]() ) of the estimating function, we have
) of the estimating function, we have
![]()
Together, we thus have that the variance of the OLS estimator ![]() is equal to
is equal to
![]()
The matrix ![]() is the population (true) expectation of the product of the vector X with its transpose. Similarly,
is the population (true) expectation of the product of the vector X with its transpose. Similarly, ![]() denotes the population error variance. To estimate the variance in practice, we can use the expression in the previous equation, replacing
denotes the population error variance. To estimate the variance in practice, we can use the expression in the previous equation, replacing ![]() by its usual sample estimate,
by its usual sample estimate, ![]() . The matrix
. The matrix ![]() can be estimated by its empirical (sample) mean
can be estimated by its empirical (sample) mean

The variance of the OLS estimator ![]() can thus be estimated by
can thus be estimated by
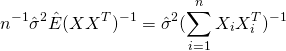
With a little bit of manipulation (which I won’t show here), we can see that this is identical to the variance estimator used in OLS implementations, i.e.
![]()
We have thus shown that the usual OLS variance estimator, derived assuming the covariates are fixed, is a consistent estimator of the variance of OLS in repeated sampling in which the covariates are random.
In a future post, I’ll look at how the preceding derivations can be extended to the case where we relax the assumption that the errors have constant variance.
A simple semiparametric model
A final note. If the model only consists of the assumptions that ![]() and that the errors have constant variance, the model is termed semiparametric. This is because although we have specified a certain aspect of the distribution of the observable random variables (specifically, how the mean of Y varies as a function of X, and that the error variance is constant), all other aspects of the distribution are left arbitrary. The parametric component corresponds to the finite dimensional parameters
and that the errors have constant variance, the model is termed semiparametric. This is because although we have specified a certain aspect of the distribution of the observable random variables (specifically, how the mean of Y varies as a function of X, and that the error variance is constant), all other aspects of the distribution are left arbitrary. The parametric component corresponds to the finite dimensional parameters ![]() and
and ![]() , whilst the non-parametric component corresponds to all the other aspects of the joint distribution of Y and X which we have left arbitrary.
, whilst the non-parametric component corresponds to all the other aspects of the joint distribution of Y and X which we have left arbitrary.
Thank you for an interesting post! I am a self-taught in statistics, so please bear with me if I seem to talk garbage !
Under the assumption that regressors can be random variables, are there methods in statistical literature that use regressors as dependent variables along with the original response variable (multivariate response)? One could then have a model for the original response variable (y) with parameter vector (P) and a sub-model for the regressors (x) with a parameter vector (B). In that way the variance covariance matrix would directly correlate the parameter vectors P and B where the diagonal elements would represent the variance of the parameters and the off-diagonals would give us an estimate of the effect of regressor on the original response variable (y).
The sub-model for the regressor would have an estimated mean equal to the sample mean and the variance representing the sample standard deviation (under the assumption that the regressor is measured error free – no noise).
My dilemma is – how to use the covariance between the regressor and response parameters to get an estimate of the “regression coefficient” where one unit of change in regressor will change the response y by “coefficient times”
Again, please consider my non-expertise in this matter !
Thanks! You could specify (and fit) a multivariate/joint model f(Y|X,theta1)f(X|theta2), where theta1 are the parameters describing the dependence of Y on X, and theta2 are parameters describing the marginal distribution of the regressors. However, if you are only interested in the parameters in the model for Y|X, and you don’t (in your model) assume any relationship between theta1 and theta2, then there is nothing to be gained by modelling the marginal distribution of the regressors. That this is true partly justifies the common practice of treating the regressors as if they were fixed even in situations (as often occurs) that they can be considered as random as the dependent/response variable.
I’m not sure if that helps answer you question though?
On the topic of random predictors/covariates, and the fact that standard statistical theory treats predictors as fixed, I’d highly recommend looking at the following paper which I have just come across: Models as Approximations: How Random Predictors and Model Violations Invalidate Classical Inference in Regression
Hello,
I have few comments about the post in the page.
1. the letters Y and X in the section “variance” should be in boldface, as they are sampling variables and represent a colum vector and a matrix, respectively. I find kind of hard to follow the steps, written this way.
2. the variance of the OLS estimator in this page seems quite different from the one you got at the page
http://thestatsgeek.com/2013/08/30/why-regression-inference-assuming-fixed-predictors-is-still-valid-for-random-predictors/
both for random predictors. If anything, because here it tends to zero as the cardinality n of the samples tends to infinity.
How do you explain that?
3. in this page you define “residuals” what is normally called “errors”, the difference between the two being that for the
latter we use the real (unknown) parameters \beta, whereas for the former notion we use OLS estimates and the sample variable observations. The common
variance \sigma^2 is assumed for errors and not residuals, which in general have variance dependent on the sample’s index.
In this context, i do not understand what you mean by “usual sample estimate” of \sigma^2, as we do not know \beta.
If you mean estimating \sigma^2 by means of the residuals variance then i would not define it exactly as an usual sample estimate.
thanks for clarifying this.
simone
Thanks Simone for your comments/questions.
1. Sorry you find the notational convention hard to follow. I would say however that there is no standard convention for these things – indeed the book on semiparametric inference linked to in the article for example does not use boldface for random variables.
2. The variance estimator in the preceding post was:
where the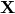 matrix is the matrix of covariate values across all n subjects. At the bottom of the current post, the penultimate variance expression does indeed involve
matrix is the matrix of covariate values across all n subjects. At the bottom of the current post, the penultimate variance expression does indeed involve  , and an expectation involving
, and an expectation involving 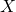 (not boldface), which indicates a randomly sampled covariate vector for an individual subject. As the text then explains, further algebraic manipulation which is not shown in the post shows that you can re-express this variance estimator as the one given in the preceding post.
(not boldface), which indicates a randomly sampled covariate vector for an individual subject. As the text then explains, further algebraic manipulation which is not shown in the post shows that you can re-express this variance estimator as the one given in the preceding post.
3. Thank you – you are right. I shall edit the post to correct this.
I am confused by the notation of X and X^T. In this article you say E(Y|X)=XTβ, which means X is a pxn matrix. In the previous article E(Y|X)=Xβ was used, where X is an nxp matrix. My understanding is that this is the normal representation of X.
Some of the following results use X as an nxp matrix, like β^=(XTX)−1XTY, while some results use X as a pxn matrix, like X(Y−XTβ).
I apologize for my math typesetting here.
Although it may not be that clear visually, the post contains both X without bold and X in bold. X without bold indicates a column vector of covariate values for an individual subject. Bold X represents the nxp matrix of covariate values across all n subjects.
Hello, thanks for that post that bring light on this topic.
I have a question that bother me, as a student of engineering.
Usually full random treatment of regressor is a topic of interest for sociologist,economist,epidemiologist etc. because covariates are ‘stocastic’ in nature, as pointed out in many books while ‘fixed’ regression model reflects the priorities of experimental method in which there’s full (?) control of dependent variables.
Even if this is really underlined in every book I red I find this assumption completely out of my comprehension.
When someone try to do regression on ohm’s law for example, you have a mathematical ‘exact’ model of the kind I = (1/R ) V .
Actually you ‘fix’ the regressor putting say a certain voltage on a system and measuring the output variable as a current.
The problem is that you have nothing special on V : it’s a variable that is influenced by a number of other variables and it’s affected by stocastic fluctuation around a true, unknown, real value.
So why in science like physics,engineering etc. full probabilistic threatment of regression is not used?
Thank you
I may have misunderstood, but you are saying that in the experiment the value of V is not really fixed by the experimenter? Rather a desired value of V is chosen and specified to the system/machinery, but in actuality the voltage realised will not be exactly equal to V due to fluctuations which presumably are due to imperfections in the device used to generate the voltage? If this is the situation, this sounds like the desired V is fixed (call it V1), but the realised value is V1+e where e is some error term. In any case, if interest lies in the conditional distribution of the dependent variable given the independent one (V), one can act like the independent variable were fixed by design for statistical inference, even if in truth it is not, as per the post. Apologies if I’ve completely misunderstood!
Is the variance formula a finite sample result or asymptotic variance?
Asymptotic.
Hi,
Thank you very much for your wonderful post. Just one thing, I am not able to see the formulas/equations in the post. I tried to load the post in different computer web browsers (Chrome, Firefox, IE) and a phone web browser (Chrome on iOS), but none of them loaded the formulas. I am not sure if anyone else experienced the same issue. But do you mind checking?
Thank you very much!
Yes other people have recently been saying the same, although it always displays fine for me (Safari or Chrome). I have just added a different LaTeX plugin and used it on this page. Could you check whether you can now see the formulas ok on this page? Thanks!